ID3, C4.5, CART and Pruning

In this post, I will discuss about some algorithms used while Training Decision Trees.

Introduction

Decision Trees are Machine Learning algorithms that is used for both classification and Regression. Decision Trees can be used for multi-class classification tasks also. Decision Trees use a Tree like structure for making predictions where each internal nodes represents the test(if attribute A takes vale <5) on an attribute and each branch represent the outcome of the test on the attribute. The leaf nodes represent the class label. Some of the popular algorithms that are used to generate a Decision tree from a Dataset are ID3, c4.5 and CART.

ID3 Algorithm

ID3 stands for Iterative Dichotomiser 3 which is a learning algorithm for Decision Tree introduced by Quinlan Ross in 1986. ID3 is an iterative algorithm where a subset(window) of the training set is chosen at random to build a decision tree. This tree will classify every objects within this window correctly. For all the other objects that are not there in the window, the tree tries to classify them and if the tree gives correct answer for all these objects then the algorithm terminates. If not, then the incorrectly classified objects are added to the window and the process continues. This process continues till a correct Decision Tree is found. This method is fast and it finds the correct Decision Tree in a few iterations. Consider an arbitrary collection of C objects. If C is empty or contains only objects of a single class, then the Decision Tree will be a simple tree with just a leaf node labelled with that class. Else consider T to be test on an object with outcomes{O₁, O₂, O₃….Ow}. Each Object in C will give one of these Outcomes for the test T. Test T will partition C into {C₁, C₂, C₃….Cw}. where Cᵢ contains objects having outcomes Oᵢ. We can visualize this with the following diagram :

Source

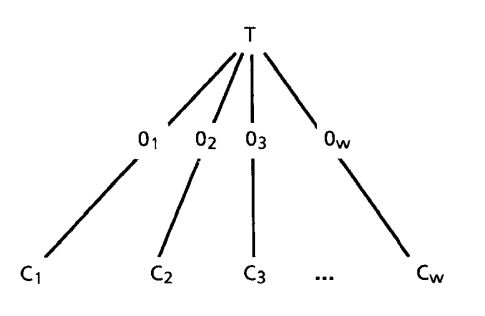
When we replace each individual Cᵢ in the above figure with a Decision Tree for Cᵢ, we would get a Decision tree for all the C. This is a divide-and-conquer strategy which will yield single-object subsets that will satisfy the one-class requirement for a leaf. So as long as we have a test which gives a non-trivial partition of any set of objects, this procedure will always produce a Decision Tree that can correctly Classify each object in C. For simplicity, let us consider the test to be branching on the values of an attribute, Now in ID3, For choosing the root of a tree, ID3 uses an Information based approach that depends on two assumptions. Let C contain p objects of class P and n of class N. These assumptions are :

A correct decision tree for C will also classify the objects in such a way that the objects will have same proportion as in C. The Probability that an arbitrary object will belong to class P is given below as :

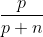
And the probability that it will belong to class N is given as :

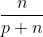
2. A decision tree returns a class to which an object belongs to. So a decision tree can be considered as a source of a message P or N and the expected information needed to generate this message is given as :

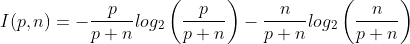
Let us consider an attribute AA as the root with values {A₁,A₂…..,Av}. Now A will partition C into {C₁,C₂…..,Cv}, where Cᵢ has those objects in CC that have a value of Aᵢ of A. Now consider Cᵢ having pᵢ objects of class P and ni objects of class N. The expected information required for the subtree for Cᵢ is I(pᵢ,nᵢ). The expected information required for the tree with A as root is obtained by :

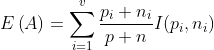
Now this is a weighted average where the weight for the i_th branch is the proportion of Objects in _C that belong to Cᵢ. Now the information that is gained by selecting A as root is given by :

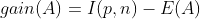
Here I is called the Entropy. So here ID3 choose that attribute to branch for which there is maximum Information Gain. So ID3 examines all the attributes and selects that A which maximizes the gain(A) and then uses the same process recursively to form Decision Trees for the subsets {C₁,C₂…..,Cv} till all the instances within a branch belong to same class.

Drawback Of Information Gain

Information gain is biased towards test with many occurances. Consider a feature that uniquely identifies each instance of a Training set and if we split on this feature, it would result in many brances with each branch containing instances of a single class alone(in other words pure) since we get maximum information gain and hence results in the Tree to overfit the Training set.

Gain Ratio

This is a modification to Information Gain to deal with the above mentioned problem. It reduces the bias towards multi-valued attributes. Consider a training dataset which contains p and n objects of class P and N respectively and the attribute A has values {A₁,A₂…..,Av}. Let the number of objects with value Aᵢ of attribute A be pᵢ and nᵢ respectively. Now we can define the Intrinsic Value(IV) of A as :

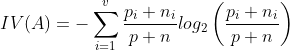
IV(A) measures the information content of the value of Attribute A. Now the Gain Ratio or the Information Gain Ratio is defined as the ratio between the Information Gain and the Intrinsic Value.

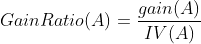
Now here we try to pick an Attribute for which the Gain Ratio is as large as possible. This ratio may not be defined when IV(A) = 0. Also gain ratio may tend to favour those attributes for which the Intrinsic Value is very small. When all the attributes are Binary, the gain ratio criteria has been found to produce smaller trees.

C4.5 Algorithm

This is another algorithm that is used to create a Decision Tree. This is an extension to ID3 algorithm. Given a training dataset S = S₁,S₂,…. C4.5 grows the initial tree using the divide-and-conquer approach as :

If all the instances in S belongs to the same class, or if S is small, then the tree is leaf and is given the label of the same class.
Else, choose a test based on a single attribute which has two or more outcomes. Then make the test as the root of the tree with a branch for each outcome of the test.
Now partition S into corresponding subsets S₁,S₂,…., based on the outcome of each case.
Now apply the procedure recursively to each of the subset S₁,S₂,….

Here the splitting criteria is Gain Ratio. Here the attributes can either be numeric or nominal and this determines the format of the test of the outcomes. If an attribute is numeric, then for an Attribute A, the test will be {A≤h, A>h}. Here h is the threshold found by sorting S on the values of A and then choosing the split between successive values that maximizes the Gain Ratio. Here the initial tree is Pruned to avoid Overfitting by removing those branches that do not help and replacing them with leaf nodes. Unlike ID3, C4.5 handles missing values. Missing values are marked separately and are not used for calculating Information gain and Entropy.

Classification And Regression Trees(CART)

This is a decision Tree Technique that produces either a Classification Tree when the dependent variable is categorical or a Regression Tree when the dependent variable is numeric.

Classification Trees :

Consider a Dataset (D) with features X = x₁,x₂….,xn and let y = y₁,y₂…ym be set of all the possible classes that X can take. Tree based classifiers are formed by making repetitive splits on X and subsequently created subsets of X. For eg. X could be divided such that {x|x₃≤53.5} and {x|x₃>53.5}. Then the first set could be divided further into X₁ = {x|x₃≤53.5, x₁≤29.5} and X₂={x|x₃≤53.5, x₁>29.5} and the other set could be split into X₃ = {x|x₃>53.5,x₁≤74.5} and X₄ = {x|x₃>53.5, x₁>74.5}. This can be applied to problems with multiple classes also. When we divide XX into subsets, these subsets need not be divided using the same variable. ie one subset could be split based on x₁ and other on x₂. Now we need to determine how to best split X into subsets and how to split the subsets also. CART uses binary partition recursively to create a binary tree. There are three issues which CART addresses :

Identifying the Variables to create the split and determining the rule for creating the split.
Determine if the node of a tree is terminal node or not.
Assigning a predicted class to each terminal node.

Creating Partition :

At each step, say for an attribute xᵢ, which is either numerical or ordinal, a subset of X can be divided with a plane orthogonal to xᵢ axis such that one of the newly created subset has xᵢ≤sᵢ and other has xᵢ>sᵢ. When an attribute xᵢ is nominal and having class label belonging to a finite set Dk, a subset of X can be divided such that one of the newly created subset has xᵢ ∈ Sᵢ, while other has xᵢ ∉ Sᵢ where Sᵢ is a proper subset of Dᵢ. When Dᵢ contains d members then there are 2ᵈ−1 splits of this form to be considered. Splits can also be done with more than one variable. Two or more continuous or ordinal variables can be involved in a linear combination split in which a hyperplane which is not perpendicular to one of the axis is used to split the subset of X. For examples one of the subset created contains points for which 1.4x₂−10x₃≤10 and other subset contains points for which 1.4x₂−10x₃>10. Similarly two or more nominal values can be involved in a Boolean Split. For example consider two nominal variables gender and results(pass or fail) which are used to create a split. In this case one subset could contain males and females who have passed and other could contain all the males and females who have not passed.

However by using linear combination and boolean splits, the resulting tree becomes less interpretable and also the computing time is more here since the number of candidate splits are more. However by using only single variable split, the resulting tree becomes invariant to the transformations used in the variables. But while using a linear combination split, using transformations in the variables can make difference in the resulting tree. But by using linear combination split, the resulting tree contains a classifier with less number of terminal nodes, however it becomes less interpretable. So at the time of recursive partitioning, all the possible ways of splitting X are considered and the one that leads to maximum purity is chosen. This can be achieved using an impurity function which gives the proportions of samples that belongs to the possible classes. One such function is called as Gini impurity which is the measure of how often a randomly chosen element from a set would be incorrectly labelled if it was randomly labelled according to the distribution of labels in the subset. Let X contains items belonging to J classes and let pᵢ be the proportion of samples labelled with class ii in the set where i∈{1,2,3….J}. Now Gini impurity for a set of items with J classes is calculated as :

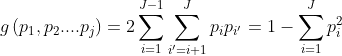
So in order to select a way to split the subset of X all the possible ways of splitting can be considered and the one which will result in the greatest decrease in node impurity is chosen.

Assigning Predicted class to Terminal Node :

To assign a class to a Terminal node a plurality rule is used : ie the class that is assigned to a terminal node is the class that has largest number of samples in that node. If there is a node where there is a tie in two or more classes for having largest number of samples, then if a new datapoint x belongs to that node, then the prediction is arbitrarily selected from among these classes.

Determining Right size of Tree :

The trickiest part of creating a Decision Tree is choosing the right size for the Tree. If we keep on creating nodes, then the tree becomes complex and it will result in the resulting Decision Tree created to Overfit. On the other hand, if the tree contains only a few terminal nodes, then the resulting tree created is not using enough information in the training sample to make predictions and this will lead to Underfitting. Inorder to determine the right size of the tree, we can keep an independent test sample, which is a collection of examples that comes from the same population or same distribution as the training set but not used for training the model. Now for this test set, misclassification rate is calculated, which is the proportion of cases in the test set that are misclassified when predicted classes are obtained using the tree created from the training set. Now initially when a tree is being created, the misclassification rate for the test starts to reduce as more nodes are added to it, but after some point, the misclassification rate for the test set will start to get worse as the tree becomes more complex. We could also use Cross-Validation to estimate the misclassification rate. Now the question is how to grow a best tree or how to create a set of candidate keys from which the best one can be selected based on the estimated misclassification rates. So one method to do this is to grow a very large tree by splitting subsets in the current partition of X even if the split doesn’t lead to appreciable decrease in impurity. Now by using pruning, a finite sequence of smaller trees can be generated, where in the pruning process the splits that were made are removed and a tree having a fewer number of nodes is produced. Now in the sequence of trees, the first tree produced by pruning will be a subtree of the original tree, and a second pruning step creates a subtree of the first subtree and so on. Now for each of these trees, misclassification rate is calculated and compared and the best performing tree in the sequence is chosen as the final classifier.

Regression Trees :

CART creates regression trees the same way it creates a tree for classification but with some differences. Here for each terminal node, instead of assigning a class a numerical value is assigned which is computed by taking the sample mean or sample median of the response values for the training samples corresponding to the node. Here during the tree growing process, the split selected at each stage is the one that leads to the greatest reduction in the sum of absolute differences between the response values for the training samples corresponding to a particular node and their sample median. The sum of square or absolute differences is also used for tree pruning.

Decision Tree Pruning

There are two techniques for pruning a decision tree they are : pre-pruning and post-pruning.

Post-pruning

In this a Decision Tree is generated first and then non-significant branches are removed so as to reduce the misclassification ratio. This can be done by either converting the tree to a set of rules or the decision tree can be retained but replace some of its subtrees by leaf nodes. There are various methods of pruning a tree. Here I will discuss some of them.

Reduced Error Pruning(REP)

This is introduced by Quinlan in 1987 and this is one of the simplest pruning strategies. However in practical Decision Tree pruning REP is seldom used since it requires a separate set of examples for pruning. In REP each node is considered a candidate for pruning. The available data is divided into 3 sets : one set for training(train set), the other for pruning(validation set) and a set for testing(test set). Here a subtree can be replaced by leaf node when the resultant tree performs no worse than the original tree for the validation set. Here the pruning is done iteratively till further pruning is harmful. This method is very effective if the dataset is large enough.

Error-Complexity Pruning

In this a series of trees pruned by different amounts are generated and then by examining the number of misclassifications one of these trees is selected. While pruning, this method takes into account of both the errors as well as the complexity of the tree. Before the pruning process, each leaves will contain only examples which belong to one class, as pruning progresses the leaves will include examples which are from different classes and the leaf is allocated the class which occurs most frequently. Then the error rate is calculated as the proportion of training examples that do not belong to that class. When the sub-tree is pruned, the expected error rate is that of the starting node of the sub-tree since it becomes a leaf node after pruning. When a sub-tree is not pruned then the error rate is the average of error rates at the leaves weighted by the number of examples at each leaf. Pruning will give rise to an increase in the error rate and dividing this error rate by number of leaves in the sub-tree gives a measure of the reduction in error per leaf for that sub-tree. This is the error-rate complexity measure. The error cost of node t is given by :

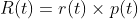
r(t) is the error rate of a node which is given as :

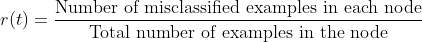
p(t) is the proportion of data at node t which is given as :

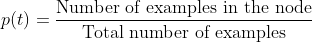
When a node is not pruned, the error cost for the sub-tree is :

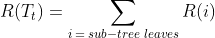
The complexity cost is the cost of one extra leaf in the tree which is given as α. Then the total cost of the sub-tree is given as :

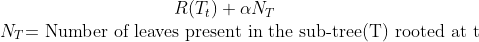
The cost of a node when pruning is done is given as :

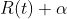
Now when these two are equal ie :

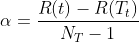
α gives the reduction in error per leaf. So the algorithm first computes αα for each sub-tree except the first and then selects that sub-tree that has the smallest value of αα for pruning. This process is repeated till there are no sub-trees left and this will yield a series of increasingly pruned trees. Now the final tree is chosen that has the lowest misclassification rate for this we need to use an independent test data set. According to Brieman’s method, the smallest tree with a mis-classification within one standard error of the minimum mis-classification rate us chosen as the final tree. The standard error of mis-classification rate is given as :

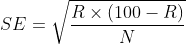
Where R is the mis-classification rate of the Pruned tree and N is the number of examples in the test set.

Minimum-Error Pruning

This method is used to find a single tree that minimizes the error rate while classifying independent sets of data. Consider a dataset with k classes and nn examples of which the greatest number(nₑ) belong to class e. Now if the tree predicts class e for all the future examples, then the expected error rate of pruning at a node assuming that each class is equally likely is given as :

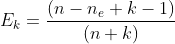
Where R is the mis-classification rate of the Pruned tree and N is the number of examples in the test set.

Now for each node in the tree, calculate the expected error rate if that sub-tree is pruned. Now calculate the expected error rate if the node is not pruned. Now do the process recursively for each node and if pruning the node leads to increase in expected error rate, then keep the sub-tree otherwise prune it. The final tree obtained will be pruned tree that minimizes the expected error rate in classifying the independent data.

Pre-pruning

This is a method that is used to control the development of a decision tree by removing the non-significant nodes. This is a top-down approach. Pre-pruning is not exactly a “pruning” technique since it does not prune the branches of an existing tree. They only suppress the growth of a tree if addition of branches does not improve the performance of the overall.

Chi-square pruning

Here a statistical test(chi-square test) is applied to determine if the split on a feature is statistically significant. Here the null hypothesis is that the actual and predicted values are independent and then a significant test is used to determine if the null hypothesis can be accepted or not. The significant test computes the probability that the same or more extreme value of the statistic will occur by chance if the null hypothesis is correct. This is called the p−value of the test and if this value is too low, null hypothesis can be rejected. For this the observed p−value is compared with that of a significance level αα which is fixed. While pruning a decision tree, rejecting null hypothesis means retaining a subtree instead of pruning it. So first a contingency table is created, which is used to summarize the relationship between several categorical variables. The structure of a contingency table is given as below :

Source

Here the rows and columns correspond to the values of the nominal attribute :

Now the chi-squared test statistic can be calculated using :

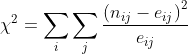
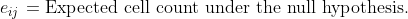
Where :

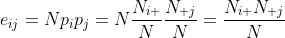
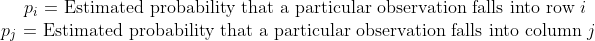
Under Null Hypothesis these probabilities are independent and so the product of these two probabilities will be the probability that an observation will fall into cell (i , j). Now consider an attribute A and under null hypothesis A is independent of Class objects. Now using the chi-squared test statistic, we can determine the confidence with which we can reject the null hypothesis ie we retain a subtree instead of pruning it. If 𝜒² value is greater than a threshold(t), then the information gain due to the split is significant. So we keep the sub-tree, and if 𝜒² value is less than the threshold(t), then the information gained due to the split is less significant and we can prune the sub-tree.

References

The following contains links to the works which helped me while writing this post. So this work is just a summary of all the below mentioned works. For further reading on all the above mentioned, please do have a look at the following :